Basic/Math
Sqrt (C++)VallistA2015. 10. 13. 11:22
sqrt 는 게임을 구현할 때나 각종 공식등을 구현할 때 많이 쓰이는 공식으로써 흔히 제곱근을 구할때 많이쓴다.
다만 우리는 기본적으로 MS에서 제공하는 것이나 각종 라이브러리에서 제공을 하므로써 내부 구현에 대해서는 잘 알질 못한다.
MS에서 기본적으로 제공하는 함수들은 무엇을 이용하는지는 모르겠지만 우리는 바빌로니아 법을 사용하여 제곱근을 구현 해볼것이다.
바빌로니아 법은 아래와 같이 근사값을 구하는 과정을 거친다.
아래는 위키 전문
-----------------------------------------------------------------------------------------------------------
양의 실수  에 대하여 다음 과정을 따라
에 대하여 다음 과정을 따라  의 근삿값을 구할 수 있다.
의 근삿값을 구할 수 있다.
- 임의의 양의 실수
 를 택한다. 이 값이
를 택한다. 이 값이  에 가까울수록 더 빨리 근삿값을 구할 수 있다.
에 가까울수록 더 빨리 근삿값을 구할 수 있다. 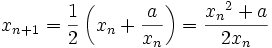
- 원하는 정밀도에 이르기까지 2의 과정을 반복한다.
위에서 구한 수열  에서 각 항은 이전 항에 비해 소수점 아래로 두 배의 유효 수치를 갖는 것으로 알려져 있으며,
에서 각 항은 이전 항에 비해 소수점 아래로 두 배의 유효 수치를 갖는 것으로 알려져 있으며, 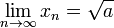 를 만족한다.
를 만족한다.
다음은  로 시작하여 위의 방법에 따라
로 시작하여 위의 방법에 따라  의 근삿값을 구한 것이다.
의 근삿값을 구한 것이다.
 는
는  의 참값과 소수점 아래 23자리까지 일치한다.
의 참값과 소수점 아래 23자리까지 일치한다.
-----------------------------------------------------------------------------------------------------------
아래는 C++ 소스코드.
'Basic > Math' 카테고리의 다른 글
| Smooth Step (C++) (0) | 2014.07.27 |
|---|---|
| Lerp (C++) (0) | 2014.07.27 |
| 거리 재기 (C++) (0) | 2014.07.27 |
| 사각형과 사각형의 충돌 (C++) (2) | 2014.07.27 |
| 원과 사각형의 충돌 (C++) (23) | 2014.07.27 |
댓글
VallistA

병특이 끝나서 게임에서 웹으로 스위칭한 프로그래머.
프로그래밍 정보등을 공유합니다.
현재는 이 블로그를 운영하지 않습니다.
vallista.kr 로 와주시면 감사하겠습니다!
자고 싶습니다. ㅠㅠ
Github :: 링크
궁금한점 문의 주시면 답변드리도록 하겠습니다
VISITED
Today :
Total :
Lately Post
Lately Comment






